Ap Calculus Bc Mixed Review Pdf Substitution Natural Log Logarithmic Differentiation
3. Derivatives
3.9 Derivatives of Exponential and Logarithmic Functions
Learning Objectives
- Notice the derivative of exponential functions.
- Notice the derivative of logarithmic functions.
- Utilise logarithmic differentiation to determine the derivative of a function.
So far, we take learned how to differentiate a variety of functions, including trigonometric, inverse, and implicit functions. In this section, we explore derivatives of exponential and logarithmic functions. As nosotros discussed in Introduction to Functions and Graphs, exponential functions play an important role in modeling population growth and the decay of radioactive materials. Logarithmic functions can help rescale large quantities and are particularly helpful for rewriting complicated expressions.
Derivative of the Exponential Function
Merely as when we found the derivatives of other functions, we can find the derivatives of exponential and logarithmic functions using formulas. As we develop these formulas, we need to brand certain basic assumptions. The proofs that these assumptions concord are across the telescopic of this class.
Showtime of all, nosotros begin with the assumption that the part ![]() , is defined for every real number and is continuous. In previous courses, the values of exponential functions for all rational numbers were defined—showtime with the definition of
, is defined for every real number and is continuous. In previous courses, the values of exponential functions for all rational numbers were defined—showtime with the definition of ![]() , where
, where ![]() is a positive integer—every bit the product of
is a positive integer—every bit the product of ![]() multiplied past itself
multiplied past itself ![]() times. Later, we defined
times. Later, we defined ![]() for a positive integer
for a positive integer ![]() , and
, and ![]() for positive integers
for positive integers ![]() and
and ![]() . These definitions leave open the question of the value of
. These definitions leave open the question of the value of ![]() where
where ![]() is an arbitrary real number. By bold the continuity of
is an arbitrary real number. By bold the continuity of ![]() , we may interpret
, we may interpret ![]() as
as ![]() where the values of
where the values of ![]() as we have the limit are rational. For example, we may view
as we have the limit are rational. For example, we may view ![]() every bit the number satisfying
every bit the number satisfying
![]()
As we see in the following table, ![]() .
.
| | | | |
|---|---|---|---|
| | 64 | | 77.8802710486 |
| | 73.5166947198 | | 77.8810268071 |
| | 77.7084726013 | | 77.9242251944 |
| | 77.8162741237 | | 78.7932424541 |
| | 77.8702309526 | | 84.4485062895 |
| | 77.8799471543 | | 256 |
We also assume that for ![]() , the value
, the value ![]() of the derivative exists. In this section, we show that by making this one boosted assumption, it is possible to prove that the function
of the derivative exists. In this section, we show that by making this one boosted assumption, it is possible to prove that the function ![]() is differentiable everywhere.
is differentiable everywhere.
Nosotros make one final assumption: that there is a unique value of ![]() for which
for which ![]() . We ascertain
. We ascertain ![]() to be this unique value, as we did in Introduction to Functions and Graphs. (Figure) provides graphs of the functions
to be this unique value, as we did in Introduction to Functions and Graphs. (Figure) provides graphs of the functions ![]() , and
, and ![]() . A visual estimate of the slopes of the tangent lines to these functions at 0 provides evidence that the value of
. A visual estimate of the slopes of the tangent lines to these functions at 0 provides evidence that the value of ![]() lies somewhere between 2.vii and 2.8. The office
lies somewhere between 2.vii and 2.8. The office ![]() is called the natural exponential office. Its changed,
is called the natural exponential office. Its changed, ![]() is called the natural logarithmic function.
is called the natural logarithmic function.
For a better estimate of ![]() , we may construct a table of estimates of
, we may construct a table of estimates of ![]() for functions of the form
for functions of the form ![]() . Earlier doing this, recall that
. Earlier doing this, recall that
![]()
for values of ![]() very close to nix. For our estimates, we choose
very close to nix. For our estimates, we choose ![]() and
and ![]() to obtain the judge
to obtain the judge
![]() .
.
Meet the following tabular array.
The testify from the table suggests that ![]() .
.
The graph of ![]() together with the line
together with the line ![]() are shown in (Figure). This line is tangent to the graph of
are shown in (Figure). This line is tangent to the graph of ![]() at
at ![]() .
.
At present that we accept laid out our basic assumptions, we begin our investigation by exploring the derivative of ![]() . Retrieve that we have assumed that
. Retrieve that we have assumed that ![]() exists. By applying the limit definition to the derivative we conclude that
exists. By applying the limit definition to the derivative we conclude that
![]() .
.
Turning to ![]() , we obtain the following.
, we obtain the following.
Nosotros come across that on the footing of the assumption that ![]() is differentiable at
is differentiable at ![]() is not only differentiable everywhere, but its derivative is
is not only differentiable everywhere, but its derivative is
![]() .
.
For ![]() . Thus, we have
. Thus, we have ![]() . (The value of
. (The value of ![]() for an arbitrary role of the class
for an arbitrary role of the class ![]() , will be derived later.)
, will be derived later.)
Derivative of the Natural Exponential Office
Let ![]() be the natural exponential function. Then
be the natural exponential function. Then
![]() .
.
In general,
![]() .
.
Derivative of an Exponential Function
Find the derivative of ![]() .
.
Solution
Using the derivative formula and the chain rule,
![]()
Combining Differentiation Rules
Observe the derivative of ![]() .
.
Solution
Use the derivative of the natural exponential part, the quotient dominion, and the chain rule.
Find the derivative of ![]() .
.
Solution
![]()
Applying the Natural Exponential Function
A colony of mosquitoes has an initial population of 1000. After ![]() days, the population is given by
days, the population is given by ![]() . Show that the ratio of the rate of modify of the population,
. Show that the ratio of the rate of modify of the population, ![]() , to the population size,
, to the population size, ![]() is constant.
is constant.
Solution
First observe ![]() . By using the chain dominion, we take
. By using the chain dominion, we take ![]() . Thus, the ratio of the charge per unit of alter of the population to the population size is given by
. Thus, the ratio of the charge per unit of alter of the population to the population size is given by
![]() .
.
The ratio of the charge per unit of modify of the population to the population size is the constant 0.3.
Derivative of the Logarithmic Function
Now that we take the derivative of the natural exponential function, we can apply implicit differentiation to find the derivative of its inverse, the natural logarithmic function.
The Derivative of the Natural Logarithmic Office
If ![]() and
and ![]() , then
, then
![]() .
.
More generally, let ![]() be a differentiable function. For all values of
be a differentiable function. For all values of ![]() for which
for which ![]() , the derivative of
, the derivative of ![]() is given past
is given past
![]() .
.
Proof
If ![]() and
and ![]() , then
, then ![]() . Differentiating both sides of this equation results in the equation
. Differentiating both sides of this equation results in the equation
![]() .
.
Solving for ![]() yields
yields
![]() .
.
Finally, we substitute ![]() to obtain
to obtain
![]() .
.
We may also derive this result by applying the inverse part theorem, as follows. Since ![]() is the inverse of
is the inverse of ![]() , by applying the inverse function theorem we have
, by applying the inverse function theorem we have
![]() .
.
Using this outcome and applying the concatenation rule to ![]() yields
yields
![]()
The graph of ![]() and its derivative
and its derivative ![]() are shown in (Figure).
are shown in (Figure).
Taking a Derivative of a Natural Logarithm
Observe the derivative of ![]() .
.
Solution
Use (Figure) directly.
Using Backdrop of Logarithms in a Derivative
Detect the derivative of ![]() .
.
Solution
At outset glance, taking this derivative appears rather complicated. However, by using the properties of logarithms prior to finding the derivative, we can make the trouble much simpler.
Differentiate: ![]() .
.
Solution
![]()
At present that we can differentiate the natural logarithmic function, nosotros tin can use this result to observe the derivatives of ![]() and
and ![]() for
for ![]() .
.
Derivatives of General Exponential and Logarithmic Functions
Let ![]() , and let
, and let ![]() exist a differentiable office.
exist a differentiable office.
- If
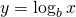 , so
, so 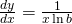 .
.More by and large, if
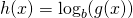 , then for all values of
, then for all values of  for which
for which 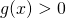 ,
,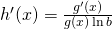 .
. - If
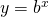 , then
, then 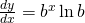 .
.More by and large, if
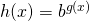 , then
, then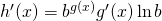 .
.
Proof
If ![]() , then
, then ![]() . Information technology follows that
. Information technology follows that ![]() . Thus
. Thus ![]() . Solving for
. Solving for ![]() , we take
, we take ![]() . Differentiating and keeping in mind that
. Differentiating and keeping in mind that ![]() is a abiding, we meet that
is a abiding, we meet that
![]() .
.
The derivative in (Figure) now follows from the chain dominion.
If ![]() , so
, so ![]() . Using implicit differentiation, once more keeping in mind that
. Using implicit differentiation, once more keeping in mind that ![]() is constant, it follows that
is constant, it follows that ![]() Solving for
Solving for ![]() and substituting
and substituting ![]() , we come across that
, we come across that
![]() .
.
The more than general derivative ((Effigy)) follows from the chain rule. ![]()
Applying Derivative Formulas
Detect the derivative of ![]() .
.
Solution
Use the quotient rule and (Figure).
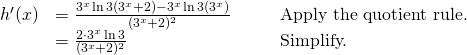
Finding the Slope of a Tangent Line
Find the slope of the line tangent to the graph of ![]() at
at ![]() .
.
Solution
To notice the slope, we must evaluate ![]() at
at ![]() . Using (Figure), we encounter that
. Using (Figure), we encounter that
![]() .
.
By evaluating the derivative at ![]() , we see that the tangent line has slope
, we see that the tangent line has slope
![]() .
.
Find the slope for the line tangent to ![]() at
at ![]() .
.
Solution
![]()
Logarithmic Differentiation
At this point, we can take derivatives of functions of the form ![]() for certain values of
for certain values of ![]() , too every bit functions of the form
, too every bit functions of the form ![]() , where
, where ![]() and
and ![]() . Unfortunately, we notwithstanding do not know the derivatives of functions such as
. Unfortunately, we notwithstanding do not know the derivatives of functions such as ![]() or
or ![]() . These functions crave a technique called logarithmic differentiation, which allows us to differentiate any function of the grade
. These functions crave a technique called logarithmic differentiation, which allows us to differentiate any function of the grade ![]() . It can also be used to catechumen a very complex differentiation trouble into a simpler i, such as finding the derivative of
. It can also be used to catechumen a very complex differentiation trouble into a simpler i, such as finding the derivative of ![]() . Nosotros outline this technique in the following trouble-solving strategy.
. Nosotros outline this technique in the following trouble-solving strategy.
Using Logarithmic Differentiation
Find the derivative of ![]() .
.
Solution
Use logarithmic differentiation to observe this derivative.
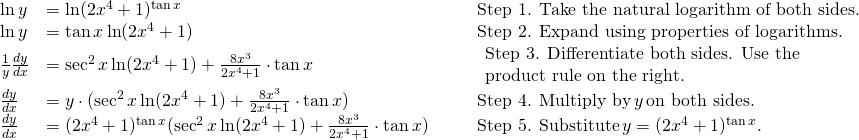
Using Logarithmic Differentiation
Observe the derivative of ![]() .
.
Solution
This problem really makes use of the properties of logarithms and the differentiation rules given in this affiliate.

Extending the Power Rule
Detect the derivative of ![]() where
where ![]() is an arbitrary existent number.
is an arbitrary existent number.
Solution
The procedure is the aforementioned as in (Effigy), though with fewer complications.

Use logarithmic differentiation to find the derivative of ![]() .
.
Solution
![]()
Find the derivative of ![]() .
.
Solution
![]()
Key Concepts
Fundamental Equations
For the following exercises, find ![]() for each function.
for each function.
1. ![]()
Solution
![]()
two. ![]()
three. ![]()
Solution
![]()
iv. ![]()
five. ![]()
Solution
![]()
6. ![]()
7. ![]()
Solution
![]()
viii. ![]()
ix. ![]()
Solution
![]()
ten. ![]()
11. ![]()
Solution
![]()
12. ![]()
13. ![]()
Solution
![]()
14. ![]()
xv. ![]()
Solution
![]()
For the post-obit exercises, utilize logarithmic differentiation to find ![]() .
.
16. ![]()
17. ![]()
Solution
![]()
18. ![]()
19. ![]()
Solution
![]()
twenty. ![]()
21. ![]()
Solution
![]()
22. ![]()
23. ![]()
Solution
![]()
24. [T] Observe an equation of the tangent line to the graph of ![]() at the point where
at the point where
![]() . Graph both the office and the tangent line.
. Graph both the office and the tangent line.
25. [T] Find the equation of the line that is normal to the graph of ![]() at the point where
at the point where ![]() . Graph both the function and the normal line.
. Graph both the function and the normal line.
Solution

![]()
29. [T] The population of Toledo, Ohio, in 2000 was approximately 500,000. Presume the population is increasing at a rate of 5% per year.
- Write the exponential function that relates the total population as a role of
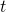 .
. - Use a. to determine the rate at which the population is increasing in
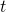 years.
years. - Use b. to determine the rate at which the population is increasing in x years.
Solution
a. ![]() individuals
individuals
b. ![]() individuals per year
individuals per year
c. 39,737 individuals per year
Solution
a. At the beginning of 1960 there were 5.3 thousand cases of the disease in New York Urban center. At the beginning of 1963 there were approximately 723 cases of the disease in New York City.
b. At the commencement of 1960 the number of cases of the disease was decreasing at rate of -4.611 1000 per year; at the start of 1963, the number of cases of the disease was decreasing at a rate of -0.2808 thousand per year.
For the following exercises, use the population of New York Metropolis from 1790 to 1860, given in the post-obit table.
| Years since 1790 | Population |
| 0 | 33,131 |
| 10 | 60,515 |
| 20 | 96,373 |
| 30 | 123,706 |
| 40 | 202,300 |
| 50 | 312,710 |
| sixty | 515,547 |
| 70 | 813,669 |
33. [T] Using a figurer program or a calculator, fit a growth curve to the information of the form ![]() .
.
Solution
![]()
34. [T] Using the exponential best fit for the data, write a table containing the derivatives evaluated at each year.
35. [T] Using the exponential best fit for the data, write a table containing the second derivatives evaluated at each year.
Solution
| Years since 1790 | |
|---|---|
| 0 | 69.25 |
| 10 | 107.5 |
| 20 | 167.0 |
| 30 | 259.4 |
| 40 | 402.eight |
| 50 | 625.5 |
| lx | 971.four |
| 70 | 1508.5 |
36. [T] Using the tables of commencement and second derivatives and the best fit, answer the post-obit questions:
- Volition the model be accurate in predicting the future population of New York City? Why or why not?
- Estimate the population in 2010. Was the prediction correct from a.?
Glossary
- logarithmic differentiation
- is a technique that allows u.s. to differentiate a office by first taking the natural logarithm of both sides of an equation, applying properties of logarithms to simplify the equation, and differentiating implicitly
Source: https://opentextbc.ca/calculusv1openstax/chapter/derivatives-of-exponential-and-logarithmic-functions/
Post a Comment for "Ap Calculus Bc Mixed Review Pdf Substitution Natural Log Logarithmic Differentiation"